各位未来的数学工作者们,大家早上好.我们这门课叫空间解析几何,是数学专业本科生的一门专业基础课。我们使用的教材是吕林根老师编写的《解析几何》(第四版),由高教出版社出版。另外推荐两本参考书:丘维声的《解析几何》(第三版)和尤承业的《解析几何》,二者都是北大出版社出版的。
今天是我们空间解析几何的第一次课.我们就从第一章说起.第一章的核心其实是在讲向量空间.它又可以分成两部分,后五节讲的是向量空间的度量结构,前五节讲的是向量空间的线性结构.
前五节线性结构又可以分为两部分:1.1节-1.3节讨论线性运算,1.4节-1.5节讨论线性关系与坐标系.
graph LR;
A("第一章 向量和坐标")-->B("1.1节~1.5节 线性结构");
B-->C("1.1节~1.3节 线性运算");
B-->D("1.4节~1.5节 线性关系与坐标系");
A-->E("1.6节~1.10节 度量结构");
E-->F("内积、外积、混合积、双重外积");
这次课我们讨论向量的线性运算,主要内容包括:向量的定义,向量的加法,向量的数乘.
有同学可能有想法了:我们在中学已经学过了这些内容了啊
既然如此,那么就请你们思考几个问题吧:
学生答:圆锥曲线
学生答:平面直角坐标系
学生答:两条相互垂直的数轴,垂足是原点,两条数轴的单位长度一样.
教师答:对某些问题而言不垂直的坐标轴反而更方便
教师答:两个单位长度必须一样吗?如果不影响问题的解决,也许会更有利哦
- 在立体空间中能不能建立坐标系?能建立什么样的坐标系?
教师答:高中学过空间直角坐标系,但它同样不是惟一的选择
- 为什么平面上的坐标系有两个坐标轴,而立体空间中的坐标系有三个坐标轴?
教师答:有同学说因为平面是2维的,立体是3维的.那么什么叫2维,什么叫3维?`
- 超越我们直观体验的4维空间、5维空间、甚至n维空间应该如何刻画呢?
教师答:所有这些问题归根结底都是坐标系的问题!
那么对于上述纷繁复杂的各种坐标系,我们能否建立一个严密而又统一的数学理论,来回答如下问题呢:
坐标系为什么可以建立起来?又是如何建立起来的呢?
这其实是我们第一章前五节所要解决的根本问题.
要想解决这个问题,我们首先应该思考一下:我们要用坐标系来干什么?或者说,坐标系的本质作用是什么?比如平面坐标系,它究竟起了什么作用?
[讨论后,教师回答]它的作用在于使用有限手段,也就是两个参数,来描述平面上任何一个点.而平面上的点,也就是平面上的位置.平面上有多少个位置呢?无限多个.所以坐标系的本质作用在于以有限描述无限.描述无限个什么?无限个位置!
那么,我们在日常生活中是如何描述某个位置的呢?
比如,你现在正在下图中的A点处沿着马路向东行走,这时候有个人向你问路,问你B怎么走.你会怎么描述B的位置呢?
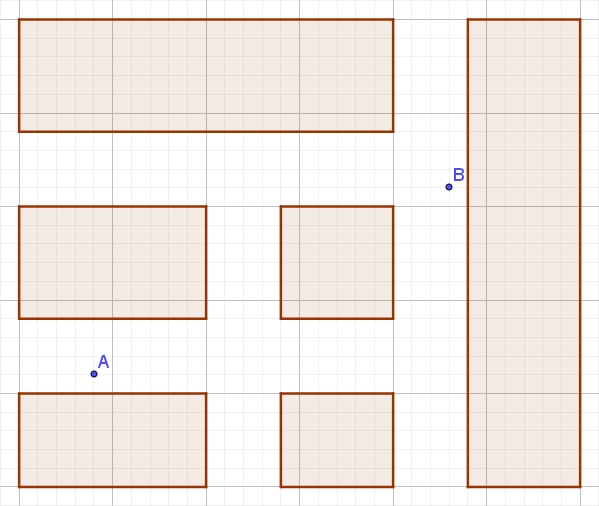
你可能会说:顺着我走的这个方向,见到第一个十字路口左拐,一直走,等见到三叉路口了就右拐,走到头就看到B了.
也就是这个路线:
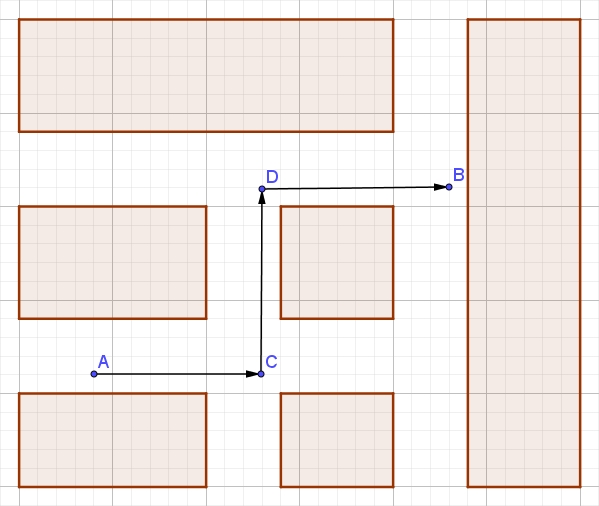
实际上,如果以A为参考点,我们可以使用这个方式描述出这个地图中任何一点的位置.那么我们使用的是什么方式呢?
我们无非是使用了几条首尾相接的有向线段,这就是你们中学所学过的向量
那么,在描述点的位置时,为什么我们不直接用点呢?
点有一个致命的问题,点的集合是松散的、没有结构的,点与点的相互关系必须借助于其他几何对象实现.而向量则不同.某些向量的集合,它们在直观上带有一种结构.以上图为例,我们实际要得到的是B的位置,实际上我们本来只需要向量AB就够了,但是城市交通让我们不能沿直线到达B,于是我们使用了向量AC、CD和DB.事实上,这三个向量恰好等效于向量AB,这正是我们中学所学过的向量加法.换句话说,向量之间的运算,将不同向量联系了起来,从而使向量的集合产生了结构.即,运算产生了结构.
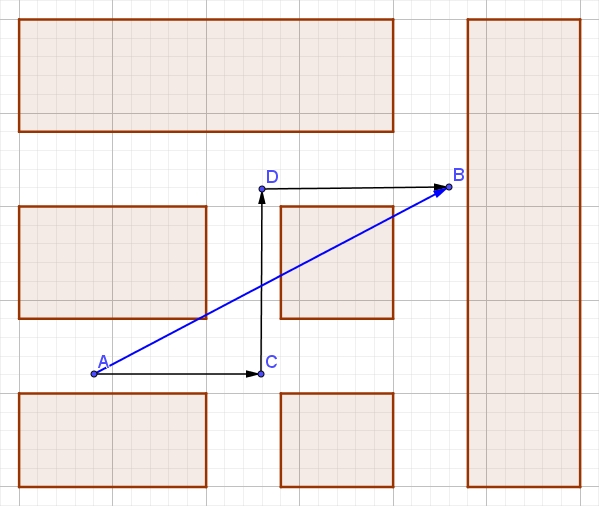
我们这里要探讨坐标系是如何构造起来的,我们需要研究的运算有两种,其一就是上面提到的向量加法.但是只有向量加法,我们并不能实现以有限描述无限.我们还需要一种运算,就是你们中学所学的向量数乘.这两种运算合称线性运算.这次课我们将系统地回顾和学习向量的加法与数乘这两种线性运算.下次课我们就要探究一下,线性运算是如何实现以有限描述无限的.
首先我们从向量的定义开始,虽然你们中学已经学过,但是我们的数学是需要体系化的,任何一个概念,如果它众所周知,那么我们可以将其作为基本概念,而不加定义,比如,点、直线、平面;而其他概念,则都应该从定义出发.
向量,就是既有大小又有方向的量.更具体一点说,在我们空间解析几何这门课上,向量就是用有向线段来表示的,而有向线段的起点和终点分别就是对应向量的起点和终点.那么接下来,如何书写向量呢?课本上使用了粗体的英文字母,但是我要求你们手写的时候,必须给它头上戴上箭头,例如a,否则将无法与实数相区分.如果已经明确了起点和终点,我们还可以用起点和终点表示向量,同样地,必须戴上箭头,例如AB.
我们刚才说了向量是既有大小又有方向的量,一个向量的大小,也被称为向量的模,也就是对应有向线段的长度,因此也称为向量的长度.向量a的模,记作∣a∣.
- 模为零的向量叫做零向量,记作0,其方向任意,不确定
- 模为1的向量叫做单位向量,向量a方向上的单位向量记作a0
前面说到,模和方向是向量的两大要素,所以我们作如下定义.
模相等、方向相同的两个向量为相等的向量;而模相等、方向相反的两个向量则叫做相反向量,其中一个称为另一个的反向量,向量a的反向量记作−a.
由向量相等的定义可以看出:平移不改变向量.所以对两个向量而言,平行和共线是一回事.
一般来说,平行于同一直线的一组向量叫做共线向量;平行于同一平面的一组向量叫做共面向量.对于这二者,后面我们会给出更深刻的刻画.
由于零向量方向不定,所以零向量可以和任何共线的向量组共线,也可以和任何共面的向量组共面.
我们在前面的“问路问题”中,已经见识过了向量的加法.下面给出严格的定义.
设已知向量a和b以及空间中任意一点O.作OA=a,AB=b.记向量OB=c.我们定义c叫做a和b的和,记作c=a+b.
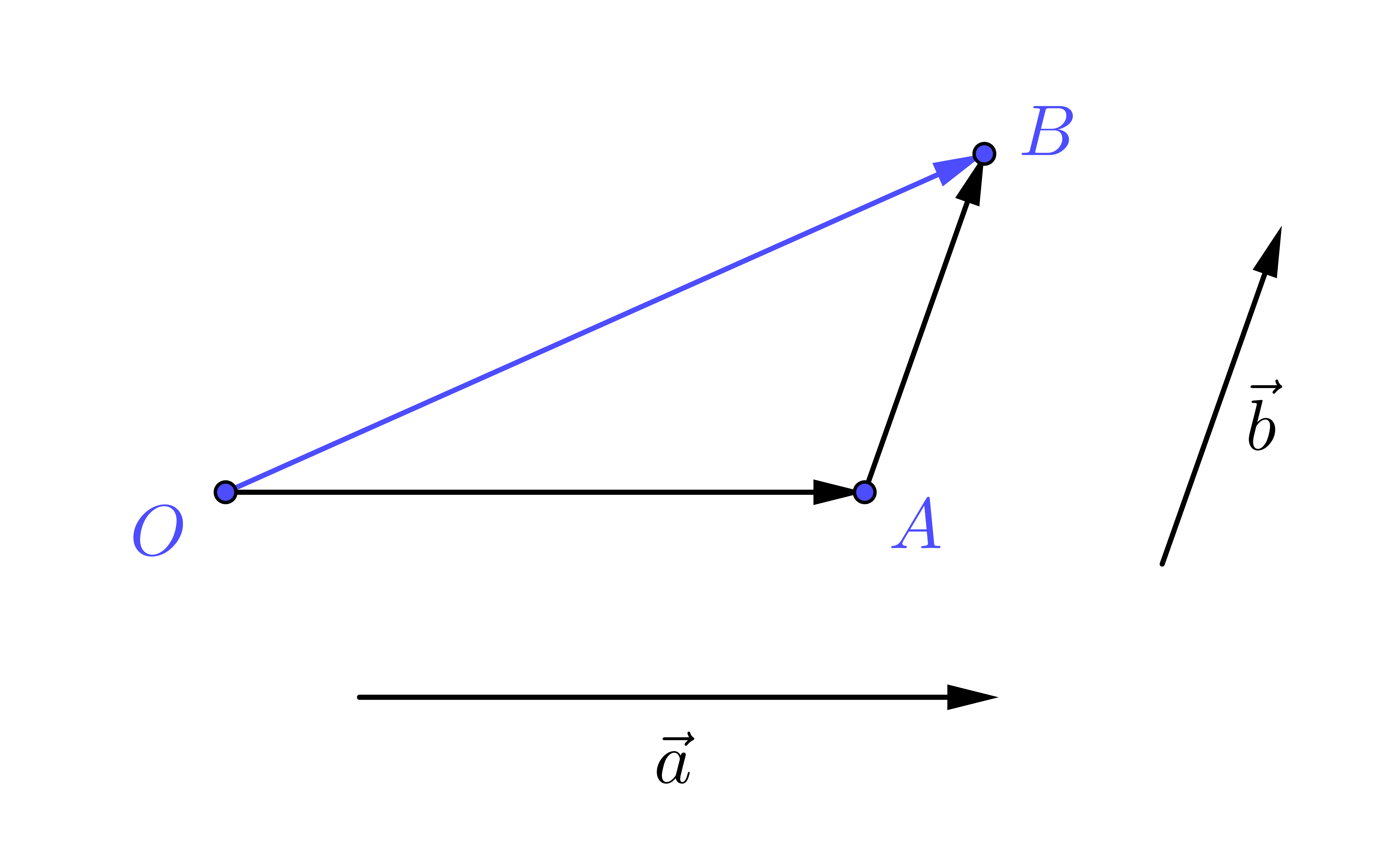
向量加法的上述定义也称为向量加法的三角形法则.
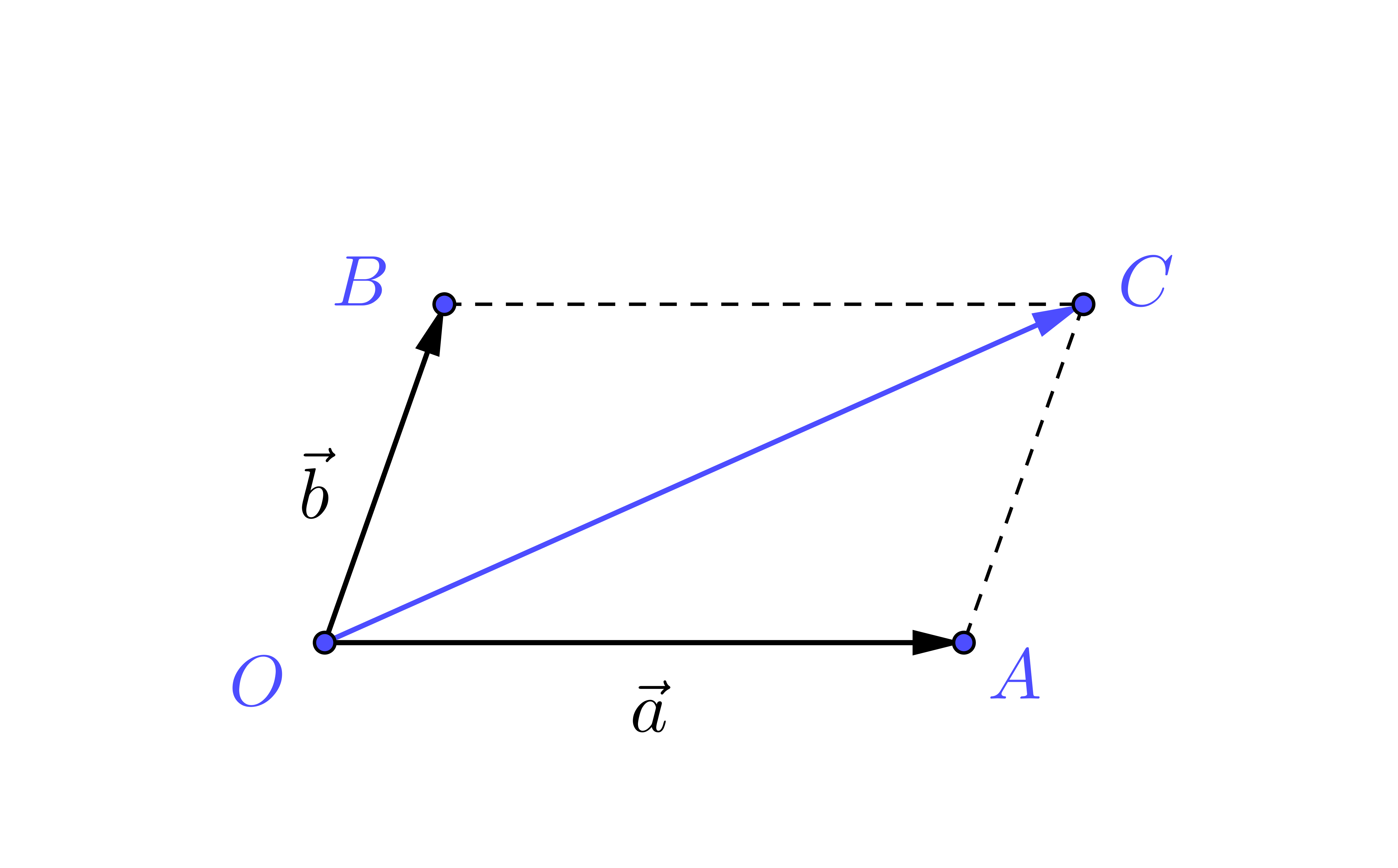
如果我们不是将向量a和b首尾相接,而是将它们的起点归结于一点,我们很容易证明下面的平行四边形法则.
定理 1.2.1 (向量加法的平行四边形法则) 如果以两个向量OA和OB为邻边作平行四边形OACB,那么对角线向量OC=OA+OB.
从向量加法的定义(即三角形法则)和平行四边形法则出发,可以很容易证明,向量加法满足如下四条运算律.
定理 1.2.2 (向量加法的运算律)
- 交换律:a+b=b+a;
- 结合律:(a+b)+c=a+(b+c);
- 零向量律:a+0=a;
- 反向量律:a+(−a)=0.
需要指出的一点是,运算不是天然的,是我们定义出来,所以运算律也不是天然的,应该由定义和其他已知理论证明出来.我们第四次课就会遇到不满足交换律和结合律的运算,所以建议大家课下自行证明这四个运算律.
尤其需要指出的是结合律.由于结合律的成立,所以多个向量求和的时候可以不加括号.也是因为结合律的成立,多个向量求和事实上满足多边形法则.
多个向量求和的多边形法则 设OA1=a1,A1A2=a2,...,An−1An=an.那么
a1+a2+⋯+an=OAn.
它之所以成立,是因为我们可以逐次使用三角形法则.
既然有了向量加法的定义,我们可以将向量减法定义为向量加法的逆运算,即:
如果b+c=a, 那么我们就定义c为a与b的差,记作c=a−b, 并且称运算a−b为向量a与b的减法.
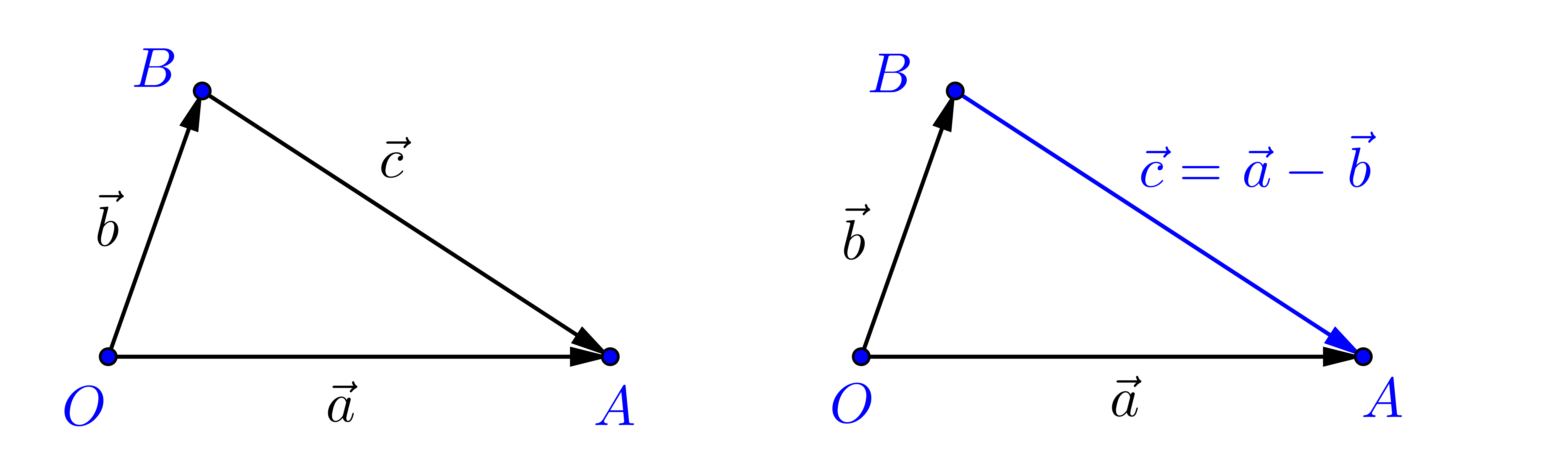
上述向量减法的定义也称为向量减法的三角形法则,只需要记住:
两个向量的差总是指向被减向量.
由于向量加法和减法都满足三角形法则,而三角形的一边之长小于等于另外两边长度之和,因而我们有如下不等式.
三角不等式
∣a±b∣≤∣a∣+∣b∣.
借助于向量减法的定义和向量加法的运算律,我们可以证明如下结论.
向量减法与反向量加法的等效性
a−b=a+(−b).
证明. 设c=a−b.
由向量减法的定义可知:c+b=a.
等式两边同时加上(−b),再由向量加法的结合律可知:
c+(b+(−b))=a+(−b).由反向量律和零向量律可知:c=a+(−b).□
我们之所以要将如此显而易见的结论的证明写下来,是为了向大家强调几件事:
- 看似平凡而直观的结论,其证明未必是平凡的,它甚至可能是错的.数学专业的学生应该养成严谨的治学态度.
- 证明的书写是有一定格式的.我们要求:
- 以“证明”二字开始,随后有一个点(注意不是冒号).
- 以□结束,□是证明结束的标志,它表示这之后的文本与此证明无关.
- 凡是命题中没有出现的名称,应该设出,例如上述证明中的c.
- 凡是添加新的操作,如辅助线等,必须以文字明确说明,禁止仅以“如图所示”等含糊的话语说明.
- 禁止一切形式的“循环论证”.
- 最后,数学证明是严谨的演绎推理.证明中每一个小结论的出现,必须要有“三段论”,即
- 大前提(所依据的理论,必须是已经证明过的正确的理论而非你的臆想)
- 小前提(条件)
- 结论.
- 其中,大前提或小前提可以酌情省略.
另外,这个证明还告诉我们一件有趣的事情:
向量等式可以移项.
前面我们已经讲向量的加法,这是两种线性运算之一.
但是只有向量加法,并不能实现我们以有限描述无限的目的,我们还需要第二种线性运算,那就是向量的数乘.
设λ是一个实数,a是一个向量.我们构造一个新向量b,满足
- ∣b∣=∣λ∣⋅∣a∣;
- 当λ>0时,b与a同向;当λ<0时,b与a反向.
那么,我们就说b是λ和a的数乘,记作b=λa.
使用向量数乘的定义,我们还能得到一个意外收获,那就是前面提到的向量a0,它是非零向量a方向上的单位向量.借助向量数乘的定义,我们可以得到如下刻画.
非零向量的单位化 若a是非零向量,那么a0=∣a∣−1a.
与向量加法类似地,向量数乘也满足四条运算律.
定理1.3.1(向量数乘的运算律) 向量数乘满足如下运算律:
- 幺律:1⋅a=a;
- 结合律:λ(μa)=(λμ)a;
- 第一分配律:(λ+μ)a=λa+μa;
- 第二分配律:λ(a+b)=λa+λb.
前三条运算律非常简单,请大家课下自行证明。需要指出的是,使用向量数乘的结合律以及非零向量的单位化,我们还能得到向量数乘的一个基本性质.
向量数乘的基本性质 若a∥b且a非零.那么存在唯一的实数λ,使得b=λa.
证明. (存在性)因为a=0,所以∣a∣=0。因为a∥b,所以a和b同向或反向。
- 如果a与b同向,则取λ=∣b∣⋅∣a∣−1,那么λa=(∣b∣⋅∣a∣−1)a=∣b∣⋅(∣a∣−1a)=∣b∣a0=∣b∣b0=b.
- 如果a与b反向,则取λ=−∣b∣⋅∣a∣−1,那么λa=(−∣b∣⋅∣a∣−1)a=−∣b∣⋅(∣a∣−1a)=−∣b∣a0=∣b∣b0=b.
(唯一性)假设存在两个不同实数λ1和λ2,使得b=λ1a并且b=λ2a,二式作差可得:0=(λ1−λ2)a,但a=0,所以λ1=λ2. □
思考:条件“a非零”能否省略?如果删除了这个条件会在什么地方出问题?
答:假如a是零向量而b不是零向量,那么这里的实数λ显然无法找到.
下面我们给出第二分配律的证明.
证明. 当λ=0、a=0或b=0时,结论是平凡的.我们不妨设上述三者都非零.如果a∥b,由于a和b都不是零向量,所以由数乘的基本性质可知,存在实数μ,使得b=μa,所以λ(a+b)=λ(a+μa).由第一分配律可知,此式=λ[(1+μ)a].由结合律可得,上式=(λ+λμ)a.由第一分配律可知,上式=λa+λμa=λa+λb.以下我们只需考虑a与b不共线的情况.
设a与b不共线.令OA=a,AB=b,那么OAB构成一个三角形,所以OB=a+b.不妨设λ>0.延长OA至A1使得OA1=λOA=λa,延长OB至B1使得OB1=λOB=λ(a+b),连接A1B1(见下图).那么△OAB与△OA1B1相似.所以AB∥A1B1,所以A1B1=λb.因此,λ(a+b)=OB1=OA1+A1B1=λa+λb. □
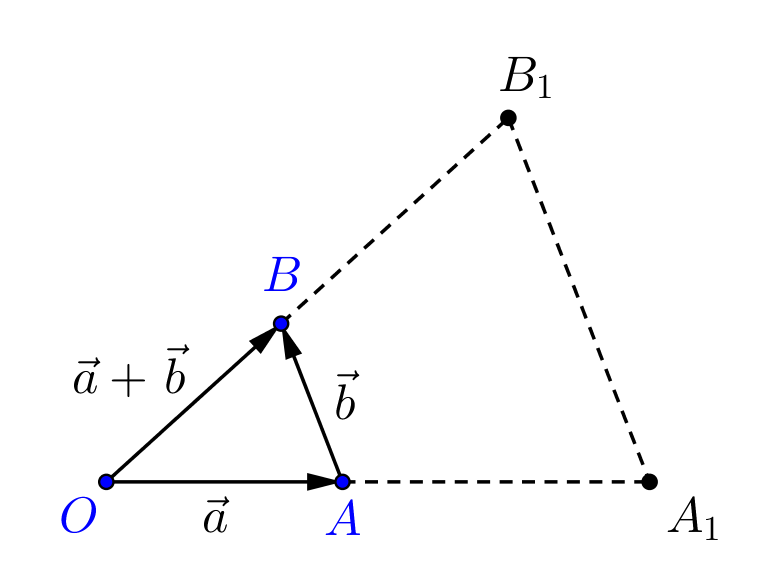
我们的证明中使用了不妨设这个词,它表示不妨设后面的内容不影响证明,或者不妨设所隐藏的证明与我们所写出的证明相似.例如我们的证明中,只是讨论了λ>0的情况,实际上λ<0的情况与此类似.请大家课下自行补充相关证明.
关于向量数乘的应用,我们看一下课本例2.
例2. 使用向量法证明:三角形两边的中位线平行于第三边,且等于第三边长度的一半.
证明. 设△ABC两边AB和AC的中点分别为M和N,那么MN=21(MA+AN)=21BA+21AC=21(BA+AC)=21BC.由数乘的定义和性质可知,MN∥BC且∣MN∣=21∣BC∣. □
请大家课下自行证明1.1节-1.3节的其他例题.
线性运算是坐标系得以建立的根本原因,下一讲我们将探究如何使用线性运算掌控无限个向量,从而建立起坐标系.
好好学习,天天向上.做好作业,下次再见!
返回《空间解析几何》









